It came upon me a month ago that I hadn't really talked about walking to uni. I'm a strange person, so I do want to talk about going to uni. Walking anywhere is interesting, because you are less constrained by roads than any other road user since you can walk across parks, jump across ditches and so on. There are many considerations when trying to get somewhere by walking. How many traffic lights are on the way? Are there any diagonals you can use to get there faster? No matter how far you walk, you'll sometimes find yourself facing what I like to call the Consecutive Traffic Lights problem.
What is this problem I've randomly given a name to? It's really simple if you look at my diagram.
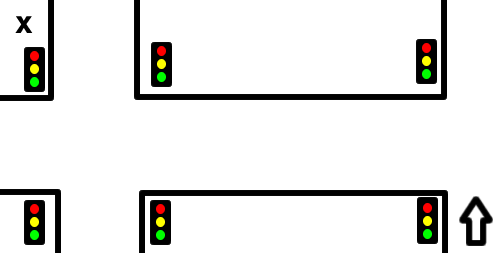
The arrow being the pedestrian, and X being the destination. If the first set of traffic lights turn green - do you cross the road at the first junction and then go to the second? If you said yes, then you have probably been wasting a lot of time waiting for traffic lights.
Why? Think of it this way. Assume the traffic lights behave independently of each other and their state when you get to them is random - and the chance of a green light in either direction (when you arrive at the lights) is 50%. This also means that the lights last an equal amount of time. As with most lights in Melbourne, crossing the junction horizontally, and then vertically or vice versa, you wait a minimal amount of time (about 15 seconds).
OK, so to my first example - the state of the first set of lights is green. Say you cross - then there is a fifty percent chance that you will get to the second set of lights in the right direction. If you don't cross - you have a 100% chance that you will get to the second set of lights in the right direction. This is just based on completely independence of the two sets of lights.
In truth (the real life scenario that I do walk every day), the lights are synced. This means that the go green in the same direction almost the same time. The problem with this? Crossing the junction and making it to the second set of lights is enough time for the second set of lights to change twice - what does this mean? There is an 80-90% chance that when you arrive at the second set of lights -> it will be red for the horizontal direction and green for the vertical direction you just crossed. Ah ha!
If you've been following this closely, you'll see that this argument doesn't hold water if you can get to the next set in three light changes - which alters the argument the other way round. However, this doesn't reduce travel time - all it changes is whether it matters that you crossed at the first traffic light or not.
This means that the dominant strategy is to ignore the first traffic light and go straight for the second set of lights, since this will probably reduce the expected travel time. Why? Since even if you don't have any information on how well the traffic lights are synchronised, you will get to cross when you arrive at the second junction. This is true as long as you can cross on all sides of the road, and some set of pedestrians can cross at any given time.